Two Point Anchor Calculators
These calculators have been recreated on new pages. They apply the same formulas. Find them through these links, or under Reference Items in the Free Content.
Related Posts
About The Author
Richard Delaney
Richard Delaney has worked professionally with ropes since 1992 as a multi-pitch rock-climbing instructor, technical rescue instructor and rope access technician. Understanding and teaching the Physics of Rigging is a core passion of Richard’s, one based on his experience, and his prior professional life as a qualified engineer.
7 Comments
Add a Comment
You must be logged in to post a comment.
How does this calculator work on a zip wire, 12 mm cable, 800 m length, 20% decline?
I measured about 2.2 tons on the upper end and 1.6 tons at the lower end.
Is this possible?
This calculator is theoretical and assumes zero mass of the line. This means that, when loaded, the lines are all straight.
For kernmantle rope systems it is reasonable to assume that the mass of the line will be swamped by the applied mass of the load.
This assumption will certainly not apply to 800m of 12mm FSWR as this will have a mass of approx. 400kg.
As for what you measured, there are too many variables to be sure, but I would certainly say it is possible.
i have a (long) question on the force calculations of an offset load on a horizontal highline.. If I enter my data into a spreadsheet I am creating for teams to have available on a tablet, the force calculations and angle come out different than what it shows here.
for example, load of 400.. 100′ span, V1 and V2 of 20′, H1 of 75, H2 of 25 the load calculations show T1 of 388.1, and T2 of 480.23. The angle at the load here shows 126.41 degrees.
However on the spreadsheet I have, using the same values show T1 of 776.209, and T2 of 320.156
(The loads and angle are equal and match when I set the load in the center of the span distance)
I am using the inverse cosine to find the angles since all three sides can easily be calculated.
lets call:
SIDES
Z=100 – the top or span
X=63.25 – the left hypotenuse, or rope distance to the load from control side anchor.
Y=44.72 – the right hypotenuse, or rope distance to the load from the static side anchor.
D=20 – the sag distance from the horizontal plane to the load suspended below.
ANGLES
ZX = a
ZY = b
XY = c
So my math to calculate angles using these values..
Z=100, X=63.25, Y=44.72, D=20.
a = arccos((x2 + z2 – y2)/2xz) = 14.9
b = arccos((y2 + z2 – x2)/2yz) = 38.7
c = arccos((x2 + y2 – z2)/2xy) = 126.41
AB=18.43, AC=26.57 and the load BC=135.
Can you share the math this example is using to calculate the anchor tension for a static load at the offset position? I have tried many different ways of using sin of the angles but I’m having a really hard time with it.. I have another document, Forces Based on Point Loads in a Catenary by Attaway, and I think i’ve read it about 50 times but the functions are a little above my comprehension.. Hope you can help out.
Thanks!
Whoops, I just noticed i had a typo but can’t edit my question.. values used were supposed to be.
I am using the inverse cosine to find the angles since all three sides can easily be calculated.
lets call:
SIDES
Z=100 – the top or span
X=77.62 – the left hypotenuse, or rope distance to the load from control side anchor.
Y=32.02 – the right hypotenuse, or rope distance to the load from the static side anchor.
D=20 – the sag distance from the horizontal plane to the load suspended below.
ANGLES
ZX = a
ZY = b
XY = c
So my math to calculate angles using these values..
Z=100, X=77.62, Y=32.02, D=20.
a = arccos((x2 + z2 – y2)/2xz) = 14.9
b = arccos((y2 + z2 – x2)/2yz) = 38.7
c = arccos((x2 + y2 – z2)/2xy) = 126.41
AB=14.9, AC=38.7 and the load BC=126.41
.
Hi Dennis,
Loads held in any position other than the neutral resting position will not work with this calculator.
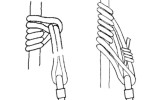
I’ve uploaded an image from my course notes showing how this works:
Richard
The deviation anchor force calculator assumes a stationary load and 100% efficiency, breaking with the assumption of a 0.2 friction coefficient from the Redirection Forces article.
To reproduce the equations used in the deviation anchor force calculator, we set exp(-mu*theta) equal to 1 for 100% efficiency. Theta is the deviation angle, and mu is the friction coefficient. The friction coefficient is therefore zero. The resultant subtends an angle of alpha = atan[(exp(mu*theta) – cos(theta)) / sin(theta)] measured counterclockwise from the horizontal.
Using theta = 75 degrees as an example, we get alpha = 37.5 degrees. Then the magnitude of the resultant is r = [(exp(-mu*theta)*sin(theta)) / cos(alpha)] = 122 % of the load, as reflected by the calculator. The force on the anchor = exp(-mu*theta) = 100% of the load.
If we instead assume a high efficiency pulley (95%), then mu = ln(1/0.95) / pi = 0.016.
alpha = atan[(exp(mu*theta) – cos(theta)) / sin(theta)] = 38.3 degrees.
r = [(exp(-mu*theta)*sin(theta)) / cos(alpha)] = 121% of load
force on anchor = exp(-mu*theta) = 98% of the load
Suppose an 85% efficient pulley. Then mu = 0.052, alpha = 40 degrees, r = 118% of the load and force on anchor = 93% of the load.
If the rope runs through an aluminum biner for 50% efficiency, then mu = 0.221, which is reasonably close to the 0.2 assumed in the Redirection Forces article.
alpha = 48.1 degrees,
r = 108% of the load,
force on the anchor = 75% of the load.
So the calculator is conservative in that it predicts higher forces than we would expect to see in actuality. The force on the anchor is not shown as an output because it is always equal to 100% of the load if we have 100% efficiency, being that mu = 0 and exp(0) = 1. For more information, see Paul Stovall’s article, Calculating Deviation Forces with Friction (http://rope-work-101.wikidot.com/rope-systems).
Absolutely correct Michael.
I guess one of the most common roped applications of this is in rope access and the rope does not move through the deviation – other than with stretch.
I am happy for the results to be conservative and that those who understand what is truly going on with the physics can do more if they choose.
Thanks,
Richard